Order of Transformations
  • All viewing and modeling transformations are represented as 4x4 matrices. 
  • Each successive glMultMatrix*() or transformation command multiplies a new 4x4 matrix M by the current modelview matrix C to yield CM. 
  • Finally, vertices v are multiplied by the current modelview matrix. 
  • This process means that the last transformation command called in your program is actually the first one applied to the vertices: CMv. 
  • Thus, one way of looking at it is to say that you have to specify the matrices in the reverse order. 

    •  

     
     
     
     
     
     
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

 Order of Transformations (cont)
  • Example:

    •  

     
     
     
     
     

    glMatrixMode(GL_MODELVIEW); 
    glLoadIdentity();
    glMultMatrixf(N); /* apply transformation N */
    glMultMatrixf(M); /* apply transformation M */
    glMultMatrixf(L); /* apply transformation L */ 
    glBegin(GL_POINTS); 
    glVertex3f(v); /* draw transformed vertex v */ 
    glEnd();
     

  •  the vertex transformation is N(M(Lv)) -that is, v is multiplied first by L, the resulting Lv is multiplied by M, and the resulting MLv is multiplied by N.
 (Actually, only a single multiplication of a vertex by the modelview matrix occurs; in this example, the N, M, and L matrices are already multiplied into a single matrix before it's applied to v.)
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

A Grand, Fixed Coordinate System
  • If you like to think in terms of a grand, fixed coordinate system-in which matrix multiplications affect the position, orientation, and scaling of your model-you have to think of the multiplications as occurring in the opposite order from how they appear in the code.

    •  
  •  Example:

    • glMatrixMode(GL_MODELVIEW); 
    glLoadIdentity(); 
    glMultMatrixf(T); /* translation */ 
    glMultMatrixf(R); /* rotation */ 
    draw_the_object();
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

A Local Coordinate System
  • Another modeling paradigm:  Objects are moved in a coodinate system local to itself.
  • With this approach transformations occur in natural order.
  •  Disadvantages: Scaling+transformation can be problimatic (local coodinates are scaled)
  •  Non-uniform scaling combined with rotations can make coordinate axes non-perpendicular

    •  

     
     
     
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Modeling Transforations
  • Although viewing transformations are applied first - most apps deal with the modeling trasformation first
  • The viewpoint is generally selected after the obects are transformed in the scene 
  •  Modeling transformations can be implemented by expressly generating the 4x4 modelview matrix and applying glMultMatrix*() to the current matrix
  •  OpenGL has transforation commands which will manipulate an object's local coordinate system

    •  

     
     
     
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Translation

void glTranslate{fd}(TYPEx, TYPE y, TYPEz); 

Multiplies the current matrix by a matrix that moves (translates) an object by the given x, y, and z values (or moves the local coordinate system by the same amounts).

    NOTE:  a translation of 0,0,0 has no effect
     
     
     
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Rotation

void glRotate{fd}(TYPE angle, TYPE x, TYPE y, TYPE z); 

    Multiplies the current matrix by a matrix that rotates an object (or the local coordinate system) in a counterclockwise direction about the ray from the origin through the point (x, y, z). The angle parameter specifies the angle of rotation in degrees.

    Rotation of 45 degrees about the Z axis
    NOTE:  Rotation of 0 degrees has no effect
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Scaling

void glScale{fd}(TYPEx, TYPE y, TYPEz); 

    Multiplies the current matrix by a matrix that stretches, shrinks, or reflects an object along the axes. Each x, y, and z coordinate of every point in the object is multiplied by the corresponding argument x, y, or z. With the local coordinate system approach, the local coordinate axes are stretched, shrunk, or reflected by the x, y, and z factors, and the associated object is transformed with them.

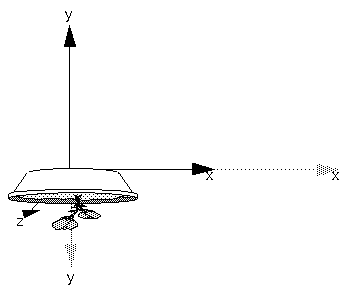
    Scale factors <  | 1.0 | reduce the size of objects
    Scale factors < 0.0 reflect the object across an axis

    NOTE!  Using glScale*() decreases the performance of lighting calculations, because the normal vectors have to be renormalized after transformation.
     
     
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Trasformation Example
  • Figure 3-8

    • glLoadIdentity(); 
    glColor3f(1.0, 1.0, 1.0); 
    draw_triangle(); /* solid lines */ 
    glEnable(GL_LINE_STIPPLE); /* dashed lines */ glLineStipple(1, 0xF0F0); 
    glLoadIdentity(); 
    glTranslatef(-20.0, 0.0, 0.0); draw_triangle(); 
    glLineStipple(1, 0xF00F);/*long dashed lines*/
    glLoadIdentity(); 
    glScalef(1.5, 0.5, 1.0); 
    draw_triangle(); 
    glLineStipple(1, 0x8888); /* dotted lines */ glLoadIdentity(); 
    glRotatef (90.0, 0.0, 0.0, 1.0); 
    draw_triangle (); 
    glDisable (GL_LINE_STIPPLE);
     
     
     
     
     
     
     

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

Homework
  • Compile the files in the "HOMEWORK" directory and become familiar with the effect of changing the different transformation parameters (makefile is included)

    •  

     

  • Applying what you know about rendering polygons and lines, render a 3D surface of the function z = sin(x) * cos(y) over the range (-3.0, -3.0) to (3.0, 3.0). You can use cube.c as a framework if you like. The command line to compile is:

    • cc -o cube cube.c -lglut -lGLU -lGL -lXmu -lXext -lX11 -lm